



Next: Algortym z wykorzystaniem macierzy
Up: Algorytm właściwy
Previous: Algorytm właściwy
Spis tresci
Algorytm znajdowania wartości własnych QR wymaga aby dana macierz
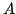 , była macierzą kwadratową
, była macierzą kwadratową
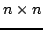 określoną na liczbach
rzeczywistych. Algorytm polega na iteracyjnym wykonywaniu
określonych czynnosci aż do otrzymania macierzy trojkątniej
górnej podobnej do macierzy
określoną na liczbach
rzeczywistych. Algorytm polega na iteracyjnym wykonywaniu
określonych czynnosci aż do otrzymania macierzy trojkątniej
górnej podobnej do macierzy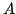 która na diagonali zawiera wartości
własne.
która na diagonali zawiera wartości
własne.
W pierwszym kroku definiujemy macierz
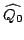 równą
macierzy jednostkowej
równą
macierzy jednostkowej
oraz macierz 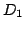 równą macierzy
równą macierzy 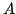
następnie wykonujemy dekompozycję macierzy 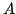 za pomocą algorytmu
dekompozycji QR, otrzymujemy
za pomocą algorytmu
dekompozycji QR, otrzymujemy
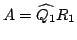 |
(1) |
gdzie macierz
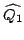 jest macierzą ortogonalną, natomiast
jest macierzą ortogonalną, natomiast
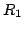 jest macierzą trójkątną górną.
Mając daną macierz
jest macierzą trójkątną górną.
Mając daną macierz
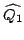 oraz traktując ją jako macierz
przejścia znajdujemy za pomocą transformacji macierzy podobnej
macierz
oraz traktując ją jako macierz
przejścia znajdujemy za pomocą transformacji macierzy podobnej
macierz 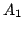 podobną do macierzy A.
podobną do macierzy A.
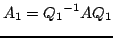 |
(2) |
mnożąc obustronnie (1) przez
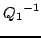 otrzymujemy:
otrzymujemy:
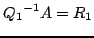 |
(3) |
łącząc (2) z (3) otrzymujemy
Jeżeli otrzymana macierz 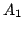 nie jest macierzą trójkątną górną
(z zadanym przybliżeniem)
to musimy przejść do kolejnego kroku iteracyjnego, w którym
przyjmujemy, że
nie jest macierzą trójkątną górną
(z zadanym przybliżeniem)
to musimy przejść do kolejnego kroku iteracyjnego, w którym
przyjmujemy, że
Ponieważ macierz 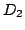 oraz
oraz 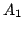 są macierzami tego samego
odwzorowana, różnią się jedynie bazami. w następnym kroku
dokonujemy dekompozycji QR obu tych macierzy, w wyniku której
otrzymujemy rownania
są macierzami tego samego
odwzorowana, różnią się jedynie bazami. w następnym kroku
dokonujemy dekompozycji QR obu tych macierzy, w wyniku której
otrzymujemy rownania
gdzie macierz 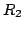 w obu przypadkach jest taka sama. Wykonując
proste obliczenia otrzymujemy macierz
w obu przypadkach jest taka sama. Wykonując
proste obliczenia otrzymujemy macierz 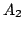
Jeżeli otrzymana macierz 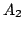 nie jest macierzą trójkątną górną
kontynuujemy interacje. Przechodząc do m-tego kroku mamy daną
macierz
nie jest macierzą trójkątną górną
kontynuujemy interacje. Przechodząc do m-tego kroku mamy daną
macierz 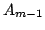 , a następnie wykonując te same operacje
otrzymujemy równania
, a następnie wykonując te same operacje
otrzymujemy równania
gdzie
natomiast 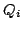 reprezentuje zmianę współrzędnych w i-tym kroku.
reprezentuje zmianę współrzędnych w i-tym kroku.
Cały algorytm można zapisać w postaci uproszczonej. Przyjmujemy
sobie w kroku zerowym, macierz 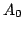 równą macierzy
równą macierzy 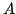 , następnie
otrzymujemy
, następnie
otrzymujemy
Przedstawiony powyżej algorytm ma jedną poważną wadę - jest mało
wydajny, algorytm ten wymaga 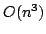 operacji mnożenia, istnieje
jednak kilka ulepszeń, które znacznie poprawiaja jego szybkość.
Metody usprawniające działanie tego algorytmu są wyjaśnione w
dalszej części pracy.
operacji mnożenia, istnieje
jednak kilka ulepszeń, które znacznie poprawiaja jego szybkość.
Metody usprawniające działanie tego algorytmu są wyjaśnione w
dalszej części pracy.
przykład:
Mając dana macierz 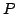 wykonujemy kolejne kroki w algorytmie.
wykonujemy kolejne kroki w algorytmie.
dokonujemy dekompozycji QR macierzy 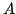
Następnie znajdujemy macierz 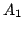 podobną do macierzy
podobną do macierzy 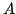 względem macierzy przejścia
względem macierzy przejścia 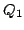 , powinna być ona równa macierzy
otrzymanej z
, powinna być ona równa macierzy
otrzymanej z 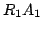 .
.
Ponieważ macierz 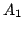 nie jest macierzą trójkątną górną
przechodzimy do następnej iteracji. Rozdzielamy używając
dekompozycji QR macierz
nie jest macierzą trójkątną górną
przechodzimy do następnej iteracji. Rozdzielamy używając
dekompozycji QR macierz 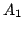 na macierz unitarną
na macierz unitarną 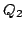 oraz
macierz trójkątkną górną
oraz
macierz trójkątkną górną 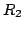
następnie obliczamy macierz 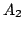
Wykonując te same obliczenia za każdym krokiem iteracyjnym macierz
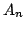 dązy do macierzy trójkątnej górnej, która na diagonali
posiada wartości własne. W powyższym przypadku wykonując 68
iteracji otrzmymamy wartości własne z dokladnością do 4 cyfry po
przecinku.
dązy do macierzy trójkątnej górnej, która na diagonali
posiada wartości własne. W powyższym przypadku wykonując 68
iteracji otrzmymamy wartości własne z dokladnością do 4 cyfry po
przecinku.




Next: Algortym z wykorzystaniem macierzy
Up: Algorytm właściwy
Previous: Algorytm właściwy
Spis tresci
2006-03-26
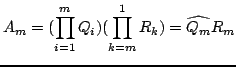
![]() operacji mnożenia, istnieje
jednak kilka ulepszeń, które znacznie poprawiaja jego szybkość.
Metody usprawniające działanie tego algorytmu są wyjaśnione w
dalszej części pracy.
operacji mnożenia, istnieje
jednak kilka ulepszeń, które znacznie poprawiaja jego szybkość.
Metody usprawniające działanie tego algorytmu są wyjaśnione w
dalszej części pracy.
![]() wykonujemy kolejne kroki w algorytmie.
wykonujemy kolejne kroki w algorytmie.
![$\displaystyle \left[ \begin{array}{ccc}
1 & 2 & 5 \cr
5 & 8 & 6 \cr
8 & 6 & 7 \cr
\end{array} \right],
$](img118.png)
![$\displaystyle A = Q_1R_1 =
\left[ \begin{array}{ccc}
-0.1054 & -0.2673 & -0.95...
...5922 \cr
0 & -3,7417 & -2,4054 \cr
0 & 0 & -3,4933 \cr
\end{array} \right]
$](img119.png)
![$\displaystyle A_1 = Q_1^{-1}AQ_1 =
\left[ \begin{array}{ccc}
14.0889 & 5.0146 ...
... & -0.9186 \cr
2.9458 & -1.8672 & 0.1968 \cr
\end{array} \right]
\equiv R_1Q_1
$](img122.png)
![$\displaystyle A_1 = Q_2R_2 =
\left[ \begin{array}{ccc}
-0.9431 & -0.1624 & -0....
... -6.3517 \cr
0 & -2.8877 & -0.8025 \cr
0 & 0 & -2.8744 \cr
\end{array} \right]
$](img124.png)
![$\displaystyle A_2 = Q_2^{-1}A_1Q_2 = R_2Q_2 =
\left[ \begin{array}{ccc}
16.632...
...15 & -0.3594 & -2.8259 \cr
0.5668 & -2.8047 & -0.2727 \cr
\end{array} \right]
$](img125.png)