



Next: Ortogonalizacja Gram-Schmidt'a
Up: Dekompozycja QR (QR factorization)
Previous: Dekompozycja QR (QR factorization)
Spis tresci
Metoda Householdera zwana również transformacją Householdera lub refleksją (odbiciem) Housoldera
jest najczęściej używaną metodą dekompozycji QR.
Kluczowym obiektem jest tutaj macierz oznaczona symbolicznie 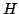 - symetryczna
i ortogonalna zwana macierzą Householdera. Jest to macierz
przekształcenia wektora, które odbija go
względem pewnej płaszczyzny. Macierz ma następującą postać:
- symetryczna
i ortogonalna zwana macierzą Householdera. Jest to macierz
przekształcenia wektora, które odbija go
względem pewnej płaszczyzny. Macierz ma następującą postać:
gdzie 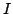 jest macierzą jednostkową oraz
jest macierzą jednostkową oraz 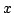 jest znormalizowanym wektorem spełniającym równanie:
jest znormalizowanym wektorem spełniającym równanie:
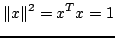
.
Użyta tutaj norma jest normą euklidesową czyli po prostu długościa wektora (jeśli jego współrzędne są rzeczywiste).
Transformacja Householdera zeruje 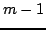 ostatnich elementów w wektorze (kolumnie) poniżej pierwszego elementu:
ostatnich elementów w wektorze (kolumnie) poniżej pierwszego elementu:
gdzie:
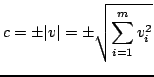
.
Łatwo sprawdzić, że:
gdzie:
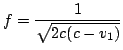
.

Aby zastosować
dekompozycję dla macierzy 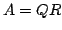 o wymiarach
o wymiarach
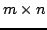 (
(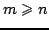 ) kontruujemy macierz
) kontruujemy macierz 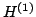 o wymiarach
o wymiarach
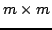 by
zamienić
by
zamienić 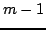 ostatnich elementów pierwszej kolumny na zera.
Podobnie skontruowana
macierz
ostatnich elementów pierwszej kolumny na zera.
Podobnie skontruowana
macierz 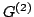 o wymiarach
o wymiarach
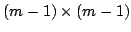 zamieni
zamieni 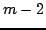 elementów drugiej kolumny na zera. Za pomocą macierzy
elementów drugiej kolumny na zera. Za pomocą macierzy 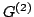 tworzymy macierz
tworzymy macierz
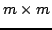 :
:
![$\displaystyle H^{(2)}=
\left [
\begin{matrix}
1 & 0 & \dots & 0 \crcr
0 \crcr
\vdots && G^{(2)} \crcr
0 \crcr
\end{matrix}\right ]$](img49.png)
.
Po 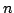 takich ortogonalnych przekształceniach (
takich ortogonalnych przekształceniach (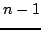 w przypadku, gdy
w przypadku, gdy 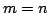 ) otrzymamy:
) otrzymamy:
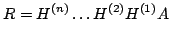
.
R jest górną macierzą trójkątną; ortogonalną macierz Q otrzymamy z iloczynu:
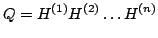
.
Z równości:
wyraźnie widać dlaczego metoda zwana jest też refleksją. W
praktyce macierze 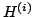 nigdy nie są jawnie liczone.
nigdy nie są jawnie liczone.




Next: Ortogonalizacja Gram-Schmidt'a
Up: Dekompozycja QR (QR factorization)
Previous: Dekompozycja QR (QR factorization)
Spis tresci
2006-03-26
![]() - symetryczna
i ortogonalna zwana macierzą Householdera. Jest to macierz
przekształcenia wektora, które odbija go
względem pewnej płaszczyzny. Macierz ma następującą postać:
- symetryczna
i ortogonalna zwana macierzą Householdera. Jest to macierz
przekształcenia wektora, które odbija go
względem pewnej płaszczyzny. Macierz ma następującą postać:
![$\displaystyle \left [ \begin{matrix}
v_1 \cr v_2 \cr \vdots \cr v_m
\end{matrix...
...ightarrow
\left [ \begin{matrix}
c \cr 0 \cr \vdots \cr 0
\end{matrix}\right ]
$](img36.png)
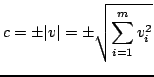 .
.
![$\displaystyle x=f
\left [
\begin{matrix}
v_1-c \cr v_2 \cr \vdots \cr v_m
\end{matrix}\right ]$](img38.png)
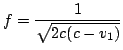 .
.![$\displaystyle H^{(2)}=
\left [
\begin{matrix}
1 & 0 & \dots & 0 \crcr
0 \crcr
\vdots && G^{(2)} \crcr
0 \crcr
\end{matrix}\right ]$](img49.png) .
.