



Next: Rotacja Givensa
Up: Dekompozycja QR (QR factorization)
Previous: Refleksja Householdera
Spis tresci
Każdy zbiór liniowo niezależnych wektorów
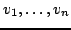 może
zostać ,,skonwertowany" do zbioru
ortogonalnych wektorów
może
zostać ,,skonwertowany" do zbioru
ortogonalnych wektorów
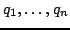 poprzez proces Gram-Schmidt'a. Rozpatrzmy sytuacje dla trzech wymiarów;
wektor
poprzez proces Gram-Schmidt'a. Rozpatrzmy sytuacje dla trzech wymiarów;
wektor  wyznacza prostą;
wektory
wyznacza prostą;
wektory  i
i 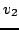 wyznaczają płaszczyznę. Wektor
wyznaczają płaszczyznę. Wektor 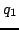 jest wektorem jednostkowym równoległym do wektora
jest wektorem jednostkowym równoległym do wektora  .
Wektor (jednostkowy)
.
Wektor (jednostkowy) 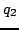 leży na płaszczyźnie wektorów
leży na płaszczyźnie wektorów  ,
,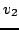 i jest normalny do wektora
i jest normalny do wektora  .
Wektor (jednostkowy)
.
Wektor (jednostkowy) 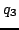 jest normalny do płaszczyzny wektorów
jest normalny do płaszczyzny wektorów  ,
, 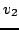 etc.
etc.
W ogólnosci przyjmujemy, że 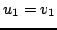 , a każdy kolejny wektor
, a każdy kolejny wektor 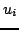 jest ortogonalny do pozostałych
jest ortogonalny do pozostałych
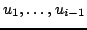 :
:
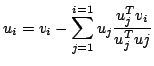
.
Baza 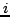 wektorów
wektorów 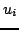 generuje tą sama podprzestrzeń co baza wektorów
generuje tą sama podprzestrzeń co baza wektorów 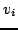 . Wektory
. Wektory
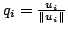 sa ortonormalne. To prowadzi do następującego twierdzenia:
sa ortonormalne. To prowadzi do następującego twierdzenia:
Każda macierz 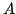 o wymiarach
o wymiarach 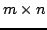 z liniowo niezależnymi kolumnami (wektorami) może być zdekomponowana
w iloczyn
z liniowo niezależnymi kolumnami (wektorami) może być zdekomponowana
w iloczyn 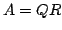 , gdzie kolumny macierzy Q są ortonormalne, a macierz R jest górna trójkątna i odwracalna.
, gdzie kolumny macierzy Q są ortonormalne, a macierz R jest górna trójkątna i odwracalna.
2006-03-26
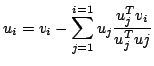 .
.
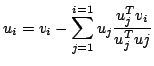 .
.