



Next: Algorytm właściwy
Up: Dekompozycja QR (QR factorization)
Previous: Ortogonalizacja Gram-Schmidt'a
Spis tresci
Niech dana będzie macierz 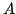 o wymiarach
o wymiarach 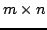 (
(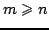 ). Dekompozycja QR wymaga wyznaczenia ortogonalnej
macierzy
). Dekompozycja QR wymaga wyznaczenia ortogonalnej
macierzy 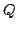 takiej, że:
takiej, że:
a 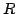 jest górną macierzą trójkątną
jest górną macierzą trójkątną 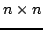 . A następnie rozwiązania układu
. A następnie rozwiązania układu 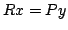 , gdzie
, gdzie 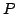 jest macierzą
jest macierzą 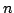 pierwszych wierszy
pierwszych wierszy 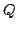 .
.
Transformacja Householdera ,,czyści" całe kolumny z wyjątkiem pierwszego elementu wektora. Jeśli chcemy ,,wyczyścić"
część macierzy zerując naraz tylko jeden element kolumny
możemy użyć rotacji Givensa, która jest szczególnie wdzięczna do
równoległej implementacji.
Macierz:
z odpowiednio dobranym
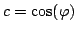 oraz
oraz
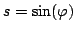 dla pewnych kątów
dla pewnych kątów 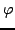 może zostać użyta do wyzerowania
elementu
może zostać użyta do wyzerowania
elementu 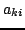 .
.
Elementy moga być zerowane kolumna po kolumnie od dołu w
następującej kolejności:
Wtedy 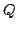 jest iloczynem
jest iloczynem
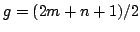 macierzy Givensa
macierzy Givensa
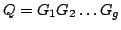 Na przykład do anihilacji dolnego elementu wektora
Na przykład do anihilacji dolnego elementu wektora 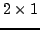 :
:
z warunków 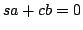 oraz
oraz 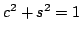 dostajemy:
dostajemy:
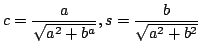
.
2006-03-26
![$\displaystyle Q^TA=\left [ \begin{matrix}R \crcr 0 \end{matrix} \right ] $](img71.png)
![$\displaystyle Q^TA=\left [ \begin{matrix}R \crcr 0 \end{matrix} \right ] $](img71.png)
![$\displaystyle G=\left [ \begin{matrix}
1 & \dots & 0 & \dots & 0 & \dots & 0 \c...
...\vdots \crcr
0 & \dots & 0 & \dots & 0 & \dots & 1 \crcr
\end{matrix} \right ] $](img74.png)
![]() oraz
oraz
![]() dla pewnych kątów
dla pewnych kątów ![]() może zostać użyta do wyzerowania
elementu
może zostać użyta do wyzerowania
elementu ![]() .
.
![$\displaystyle \left [ \begin{matrix}
c & s \crcr
-s & c
\end{matrix} \right ]^T...
...\end{matrix} \right ] =
\left [ \begin{matrix}
r \crcr 0
\end{matrix} \right ]
$](img83.png)
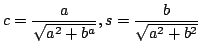 .
.