



Next: Porównanie różnych wariantów algorytmu
Up: Algorytm właściwy
Previous: Algortym z wykorzystaniem macierzy
Spis tresci
Chociaż algorytm bazujący na macierzach Hessenberga działa
znacznie szybciej od algorytmu QR w formie podstawowej to mimo
wszystko w niektórych przypadkach współczynnik zbiegania się
elementów znajdujących się na poddiagonali jest zbyt wolne. Dla
elementu
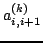 w k-tym kroku ów współczynnik wynosi
w k-tym kroku ów współczynnik wynosi
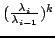 , co w przypadku gdy
wartości własne
, co w przypadku gdy
wartości własne 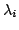 oraz
oraz
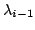 mają zbliżone
wartości jest przyczyną powolnego zbiegania się algorytmu QR do
szukanych wartości. Aby uniknąć powyższej sytuacji stosuje się w
każdym kroku iteracyjnym przesunięcia wektorów własnych
mają zbliżone
wartości jest przyczyną powolnego zbiegania się algorytmu QR do
szukanych wartości. Aby uniknąć powyższej sytuacji stosuje się w
każdym kroku iteracyjnym przesunięcia wektorów własnych
dzięki czemu współczynnik
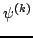 zbiegania się elementu
zbiegania się elementu
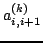 pod diagonalą jest równy
pod diagonalą jest równy
Łatwo można zauważyć, że jeżeli wartość współczynnika zbieżności
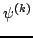 dąży do 0
to
dąży do 0
to
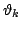 dąży do
dąży do
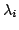 .
.
Oczywistym wnioskiem, który można wyciągnąć z powyższej zależności
jest możliwość osiągnięcia zbieżności liniowej, a nawet
kwadratowej. Algorytm polega na tym, że najpierw skupiamy się na
wartości własnej 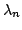 i na jego podstawie obliczamy
współczynnik
i na jego podstawie obliczamy
współczynnik
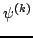 . Jeżeli
. Jeżeli 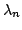 zostanie obliczona z
zadowalającą nas precyzją to przechodzimy do obliczania wartości
zostanie obliczona z
zadowalającą nas precyzją to przechodzimy do obliczania wartości
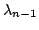 , operacje powtarzamy aż do uzyskania wszystkich
wartości własnych. Początkowo za element
, operacje powtarzamy aż do uzyskania wszystkich
wartości własnych. Początkowo za element
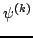 wybierano
element
wybierano
element
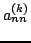 macierzy, jednakże Wilkinson w 1965 roku
zauważył, żę lepszym rozwiązaniem będzie wybranie wartości własnej
z minora o wymiarach
macierzy, jednakże Wilkinson w 1965 roku
zauważył, żę lepszym rozwiązaniem będzie wybranie wartości własnej
z minora o wymiarach
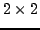 zawierającego na diagonali
wartości
zawierającego na diagonali
wartości
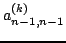 oraz
oraz
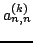 . Konsekwencją
wyboru algorytmu z przesunięciami wartości własnych jest brak
uporządkowania wartości własnych na diagonali, zazwyczaj
największe wartości własne są na początku.
. Konsekwencją
wyboru algorytmu z przesunięciami wartości własnych jest brak
uporządkowania wartości własnych na diagonali, zazwyczaj
największe wartości własne są na początku.
Algorytm QR z przesunięciami dla wcześniej zaprezentowanego
przykładu oblicza wartości własne z precyzją do 4 miejsc po
przecinku w 6 iteracjach co jest ponad 10 krotnym przyspieszeniem
i to jedynie dla macierzy 4 wymiarowej.




Next: Porównanie różnych wariantów algorytmu
Up: Algorytm właściwy
Previous: Algortym z wykorzystaniem macierzy
Spis tresci
2006-03-26
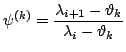
![$\displaystyle \left[ \begin{array}{ccc}
a_{n-1,n-1}^{(k)} & a_{n-1, n}^{(k)} \cr
a_{n, n-1}^{(k)} & a_{n,n}^{(k)} \cr
\end{array} \right]
$](img149.png)